Inverse Kinematics

Robot Kinematics:

Goal: Given the structure of robot arm, we can compute
- Forward Kinematics: inferring the pose of the end-effector, given the state of each joint.
- Inverse Kinematics: inferring the joint states that are necessary to reach a desired end-effector pose.

There are many ways to solve inverse kinematics, and can be categorized into two types:

Closed form (analytical) solution: a sequence or set of equations that can be solved for the desired joint angles, solves the whole system at once
- Speed: solution often computed in constant time
- Predictability: solution is selected in a consistent manner
Iterative (numerical) solution: Solved by optimization, minimize error of endeffector to desired pose
- Often in some form of Gradient Descent (a la Jacobian Transpose)
- Generality: same solver can be used for many different robots

Analytical solution

Using analytical method, each joint angle is calculated from the pose of the end-effector based on a mathematical formula. By defining the joint parameters and end-effector poses symbolically, IK can find all possible solutions of the joint angles in an analytic form as a function of the lengths of the linkages, its starting posture, and the rotation constraints.

There is no general analytical inverse kinematics solution.

All analytical inverse kinematics solutions are specific to a robot or class of robots, based on geometric intuition about the robot

Numerical solution

Using numerical solution, each joint angle is calculated iteratively using algorithms for optimization, such as gradient-based methods.

What is Jacobian?

Jacobian matrix is a matrix of partial derivatives.

The term “Jacobian” often represents both the jacobian matrix and determinants, which is defined for the finite number of function with the same number of variables. Here, each row consists of the first partial derivative of the same function, with respect to the variables. The jacobian matrix can be of any form. It may be a square matrix (number of rows and columns are equal) or the rectangular matrix(the number of rows and columns are not equal).

Jacobian Transpose

To have iterative solution, our goal is to move the endeffector to minimize error, where error means the difference between the goal state and current state.

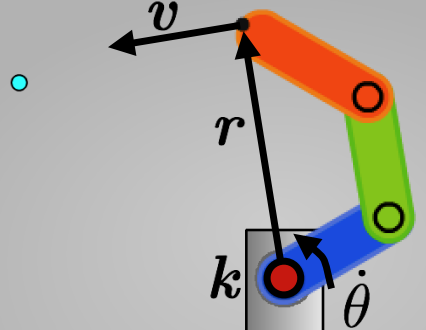
We know that when we are at x = 0m and we want to get to x = 2m, we need to move in x-direction with certain velocity to minimize the error. Now the questions is, how are linear and angular velocity related? Since the way to move the end effector in x-direction is by rotating the angle (if using revolute joint).

\[\omega = \dot{\theta}k \quad v = \omega \times r \quad v = \dot{\theta}k \times r\]

$\omega$: angular velocity of points in the frame wrt. axis k
$\dot{\theta}$: rotation speed of frame
$k$: joint rotation axis, could be [0, 0, 1] if the vector represents [x, y, k]
$v$: endeffector linear velocity
$r$: vector from joint origin to endeffector

We related the linear velocity and the angular velocity, however, what we want to know is how much change in the angle we need, now the LHS is the variable we know. To obtain joint angular velocity from endeffector linear velocity, we introduce Jacobian Transpose here.

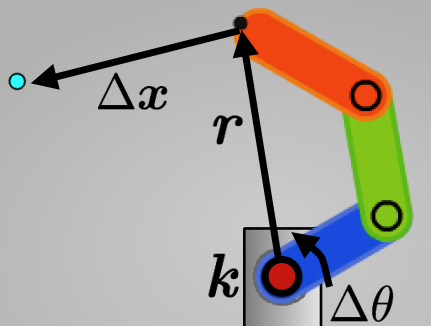
\[\Delta \theta = (k \times r)^T \Delta x\]

$(k\times r)$: Jabobian for joint i
$\Delta \theta $: Angular displacement for joint i
$\Delta x $: desired endeffector displacement

Such that to calculate the inverse kinematics, for each joint on the chain from the base link to the end effector, we firstly 1) Compute the Jacobian, then 2) Update joint angles using Jacobian transpose, finally 3) repeat the process until error minimized.

To minimize the error, we are going to use a method called Gradient descent.

Gradient descent

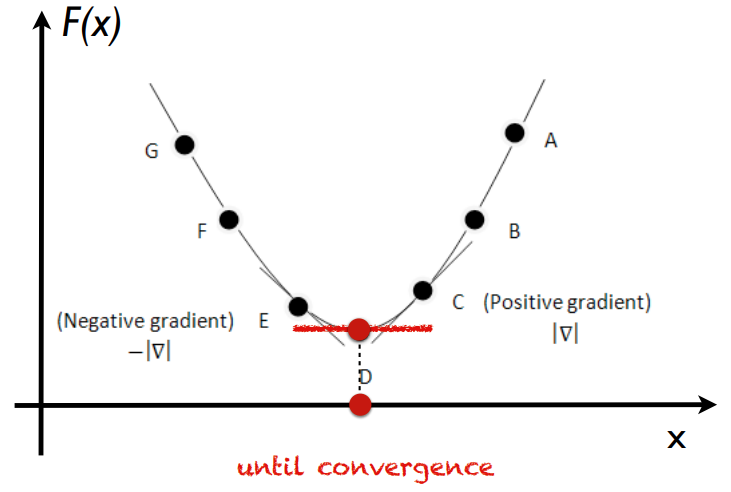
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function.

\[x_{i+1} = x_i - \gamma_i \triangledown F(x_i)\]

$\gamma_i $ is learning rate, it is the step size of each step
$\triangledown F(x_i)$ is the derivate of F(x) which is the slope of current position

Now our question becomes: What is the derivative of robot configuration? - Geometric Jacobian

Geometric Jacobian

Geometric Jacobian of the end effector is a 6-by-n matrix, where n is the number of degrees of freedom of the robot. The Jacobian maps the joint-space velocity to the end-effector velocity, relative to the base coordinate frame. The end-effector velocity equals:

\[V_{EE} = \begin{vmatrix} v_x\\ v_y\\ v_z\\ \omega_x\\ \omega_y\\ \omega_z \end{vmatrix} = J\dot{q} = J \begin{vmatrix} \dot{q_1} \\ \vdots\\ \dot{q_n} \end{vmatrix}\]

where $\omega$ is the angular velocity, $v$ is the linear velocity, and $\dot{q}$ is the vector of joint-space angle velocity.

$J$ consists of two 3-by-n matrices $J = |\frac{J_v}{J_w}|$ as shwon above. To calculate $J$ for each joint i, we have equations:

\[J_{vi} = (\{k_i\}^w - \{o_i\}^w) \times (\{p_{tool}\}^w - \{o_i\}^w)\] \[J_{\omega i} = \{k_i\}^w - \{o_i\}^w\]

Endeffector: ${p_{tool}}^w = T^w_n{p_{tool}}^n$ = the position of the end effector in world frame
Joint axis: ${k_i}^w = T^w_i{k_i}^i$ = the axis of the joint in world frame
Joint origin: ${o_i}^w = T^w_i{o_i}^i$ = the origin of the joint in world frame
All the above variables are in world frame, T is the transformation matrix.

Error Minimization by Gradient Descent using Jacobian Transpose

We first calculate the error:

\[\Delta x_n = x_d - x_n\]

Then compute the step direction:

\[\Delta q = J(q)^T \Delta x\]

Finally perform the step direction:

\[q_{n+1} = q_n + \gamma \Delta q_n\]

Jacobian Pseudoinverse

What is Pseudoinverse? - answer

For a matrix A with dimensions N x M with full rank
- Left pseudoinverse for full column rank, meaning $N \geq N$, “tall”, less than 6 DOFs
  - $A^{-1}_{left} = (A^TA)^{-1}A^T$
- Right pseudoinverse for full row rank, meaning $N \leq N$, “wide”, more than 6 DOFs
  - $A^{-1}_{right} = A^T(AA^T)^{-1}$

  
function matrix_pseudoinverse(m) {
    // returns pseudoinverse of matrix m
    var row = m.length;
    var col = m[0].length;
    var m_trans = matrix_transpose(m);

    if (row >= col) {
        return matrix_multiply(numeric.inv(matrix_multiply(m_trans, m)), m_trans);
    } else {
        return matrix_multiply(m_trans, numeric.inv(matrix_multiply(m, m_trans)));
    }
}

Error Minimization by Jacobian Pseudoinverse