Linear Algebra Refresher

In Robotics, each part of the robot’s body might has its own coordinate system. Matrix transformations are used to transform coordinate systems between the bodies and joints. And here is where linear algebra kicks in.

Linear algebra, which deals with linear equations and linear mappings in the vector space, is used for modern presentations of geometry. It is essential for representing frames of reference, rotation, translation, and general 3D homogeneous transforms.

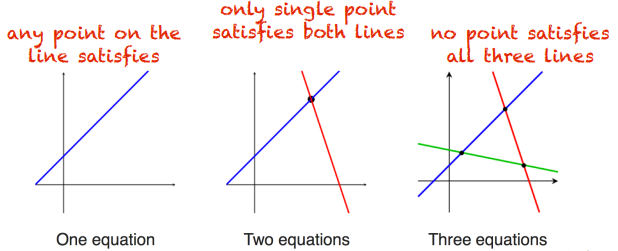
• If #unknowns > #equations, it is an underdetermined system, usually with infinite solutions
• If #unknowns < #equations, overdetermined system, usually with no solutions
• If #unknowns = #equations, usually has a unique solution

2D Example

Coordinate spaces

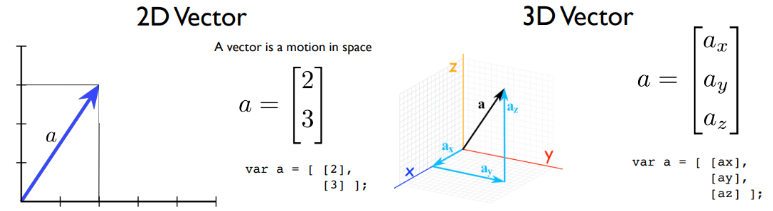
How to represent coordinates spaces as systems of linear equations? - Vector

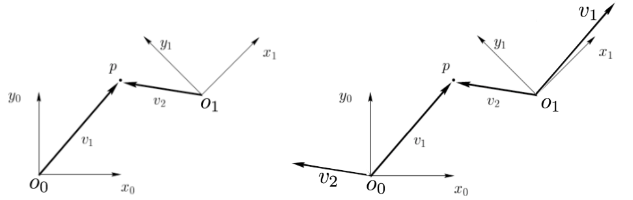
• Two coordinate frames $o_0x_0y_0$ and $o_1x_1y_1$, and a point $p$ shown in the left image.
• The location of point $p$ can be described with respect to either coordinate frame
  • $p^0 = [5, 6]^T$ and $p^1 = [-2.8, 4.2]^T$
• The vector $v_1$ is direction and magnitude from $o_0$ to $p$, and $v_2$ is from $o_1$ to $p$.
  • $v_1^0 = [5,6]^T$ - vector 1 in frame 0
  • $v_1^1 = [7.77,0.8]^T$ - vector 1 in frame 1

Vector operations

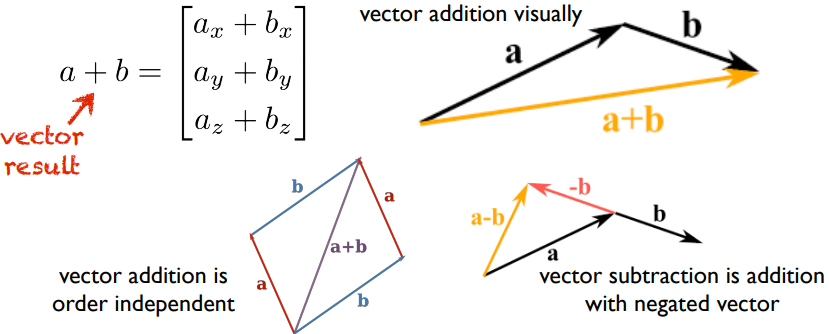
Addition and Subtraction

Magnitude and Unit Vector

• The magnitude of a vector is the square root of the sum of squares of its components:
  • $\left | a \right | = \sqrt{a_1^2+a_2^2+\cdots +a_n^2}$
• A unit vector has a magnitude of one. Normalization scales a vector to unit length.
  • $\hat{a}=\frac{a}{\left | a \right |}$

Dot Product

• $a \cdot b= a_xb_x+a_yb_y+a_zb_z=\left | a \right |\left | b \right | \cos(\theta)$
  • Dot product gives scalar result, it measures the similarity in direction of two vectors.

  

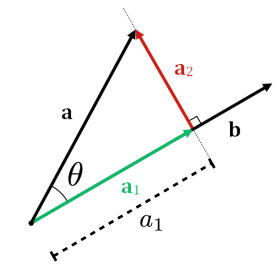
• Dot products related to projections onto vectors. Scalar projection of one vector onto another:
  • $a_1=\left | \mathrm{a} \right |\cos(\theta) = \mathrm{a} \cdot \frac{b}{\left | b \right |}= a \cdot \hat{b}$
• Vector projection is $\mathrm{a}_1=a_1\hat{b}$
• The difference is that $\mathrm{a}_1$ is a vector, and $a_1$ is a scalar. The scalar projection is using dot product, the vector projection is multiplied by a scalar.

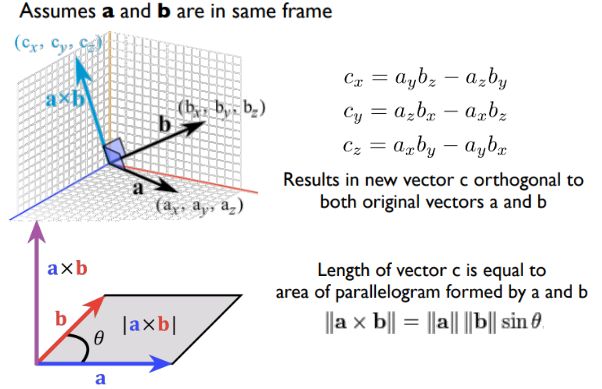
Given two vectors, how to compute a vector orthogonal to both? - Cross Product

Cross Product

Cross product denoted by $\times$, should not be confused with the dot product (projection product) which denoted by $\cdot$.

Given two linearly independent vectors $a$ and $b$, the cross product, $a \times b$ (read “a cross b”), is a vector that is perpendicular to both $a$ and $b$, and thus normal to the plane containing them.

Matrix operations

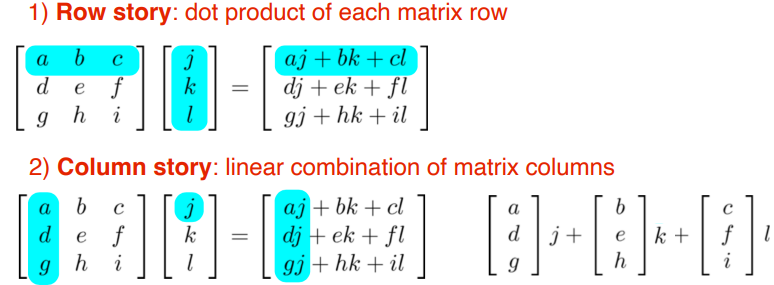
Matrix-vector multiplication

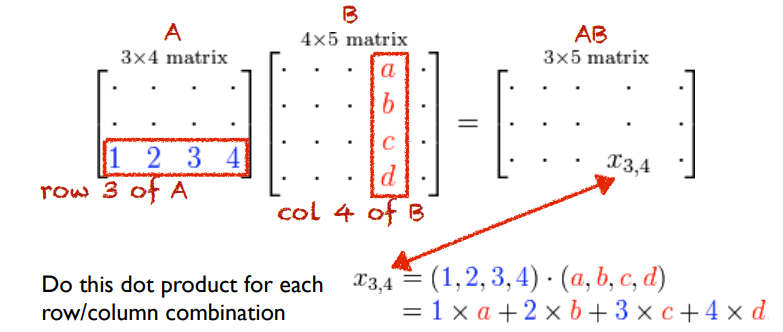
Matrix multiplication

Notes:

1. Multiplying (MxK) matrix with a (KxN) matrix will produce an (MxN) matrix
2. Matrix multiplication is not commutative: AB != BA

Resource

Great tutorial series on Linear Algebra by 3blue1brown.