RRT, RRT-connect and RRT* in Path Planning
In my first post on robotics path planning, we have discussed the graph search algorithms. As we mentioned in that post that the common approaches we have for path planning are various:
- Bug algorithms: Bug[0-2], Tangent Bug
- Graph Search (fixed graph)
- Depth first search, Breadth first search, Dijkstra, A*, Greedy best-first search
- Sampling-based Search (build graph)
- Probabilistic Road Maps, Rapidly-exploring Random Trees
- Optimization (local search)
- Gradient descent, potential fields, Wavefront
So in this post, I am going to discuss Sampling based Search - Rapidly-exploring Random Trees (RRT)
RRT
- What is RRT algorithm?
- RRT stands for Rapidly-exploring Random Tree. It is an algorithm designed to efficiently search nonconvex, high-dimensional spaces by randomly building a space-filling tree.
- An RRT grows a tree rooted at the starting configuration by using random samples from the search space. As each sample is drawn, a connection is attempted between it and the nearest state in the tree.
- Original paper: Rapidly-Exploring Random Trees: A New Tool for Path Planning
- Paper that presents the approach to trajectory planning for robots: Randomized Kinodynamic Planning
Pseudocode
As shown above, this is the basic RRT construction algorithm, and it runs for K times to keep extending the tree and return three different flags when adding new configurations. This pseudocode is from the paper for robotics planning instead of the original RRT paper.
- Firstly we initialize the tree with a initial configuration. We can either run the for loop for K times or have other conditions to stop the extending of the tree.
- The
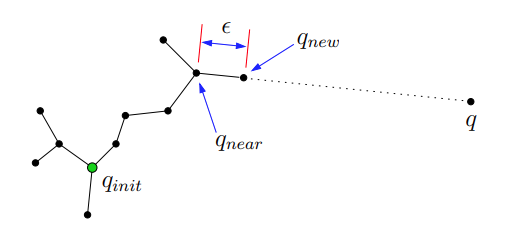
RANDOM_CONFIG()will randomly generate a configration in the C-space and assign to $q_{rand}$. Then we extend the tree from the new generated point. NEAREST_NEIGHBOR(q, T)will find a configuration $q_{near}$ in the tree that is nearest to the $q_{rand}$.- Then
NEW_CONFIGwill select a new configuration $q_{new}$ by moving an incremental distance $\epsilon$ from $q_{near}$ in the direction of $q_{rand}$. - If $q_{new}$ is valid, we add the new configuration to the tree and connected to $q_{near}$. As the image shows below.
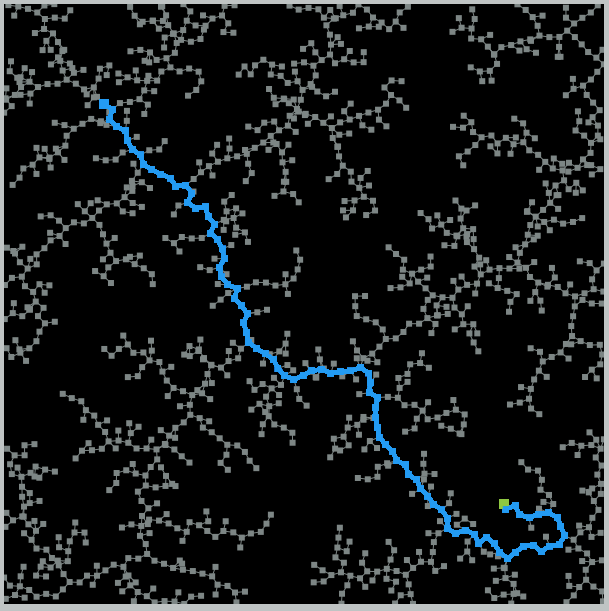
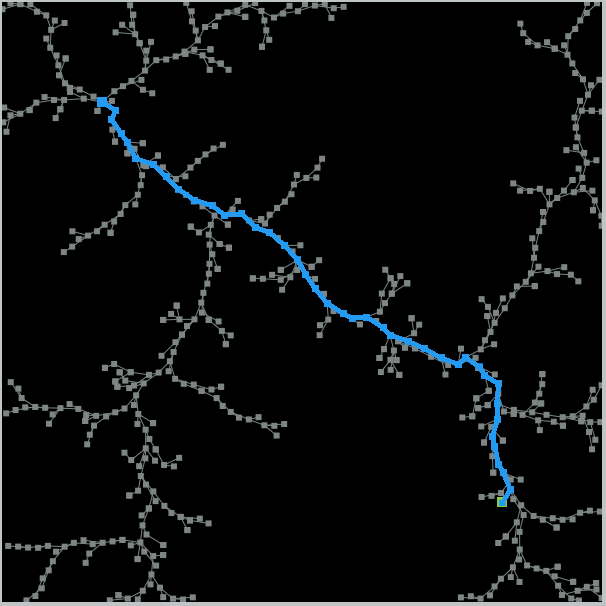
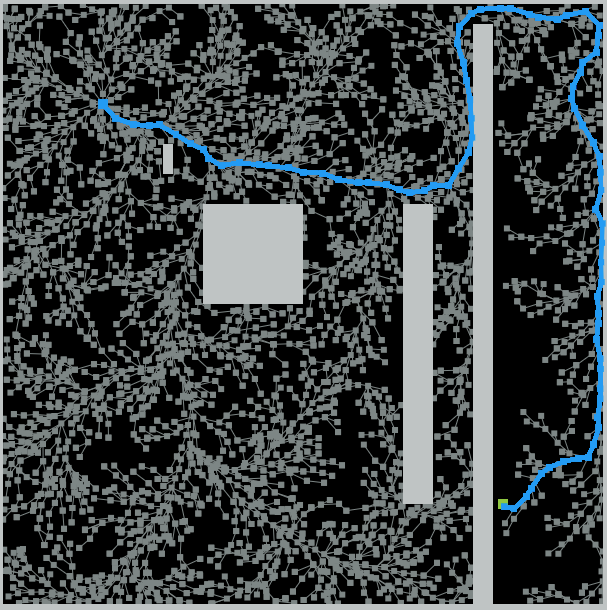
Demo
| Empty | Obstacle Map |
|---|---|
 |  |
| Iterations: 2363 | Iterations: 10000+ |
From the demo, we can tell that there is a problem with this algorithm. It is not goal-oriented. The search is so random that it takes too long to find the goal. For the obstacle map, due to the randomness, the algorithm could not find a solution within 10000 iterations, so we stopped. Though the algorithm is probabilistically complete but not optimal.
RRT-Connect
The paper RRT-Connect: An Efficient Approach to Single-Query Path Planning introduced the RRT-Connect algorithm. This algorithm combines Rapidly-exploring Random Trees (RRTs) with a simple greedy heuristic that aggressively tries to connect two trees, one from the initial configuration and the other from the goal. RRT-Connect finds solutions faster than RRT.
Pseudocode
- As shown in the image above, instead of attempting to extend an RRT by a single step, the
CONNECTheuristic iterates theEXTENDstep until q or an obstacle is reached. - Under
RRT_CONNECT_PLANNER, the two trees $T_a$ and $T_b$ are maintained at all times until they become connnected and a solution is found. - One tree keeps extending until
- Reach the goal and return the solution, or
- Hit obstacles and swap the two trees. For example, if it was $T_a$ extending, then it is $T_b$’s turn to grow.
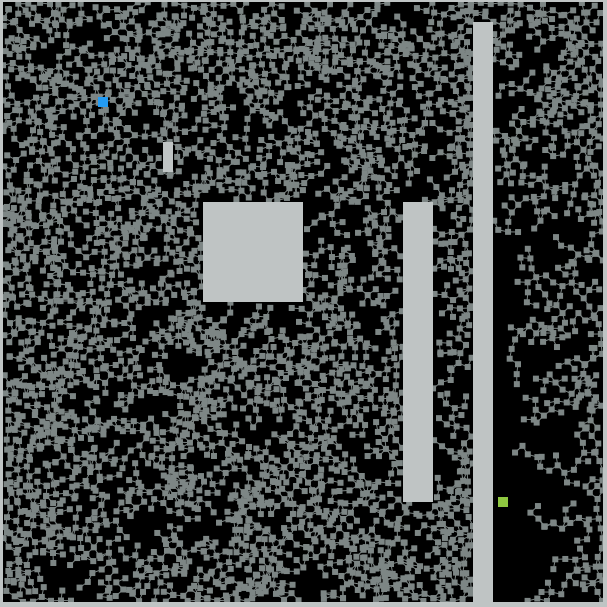
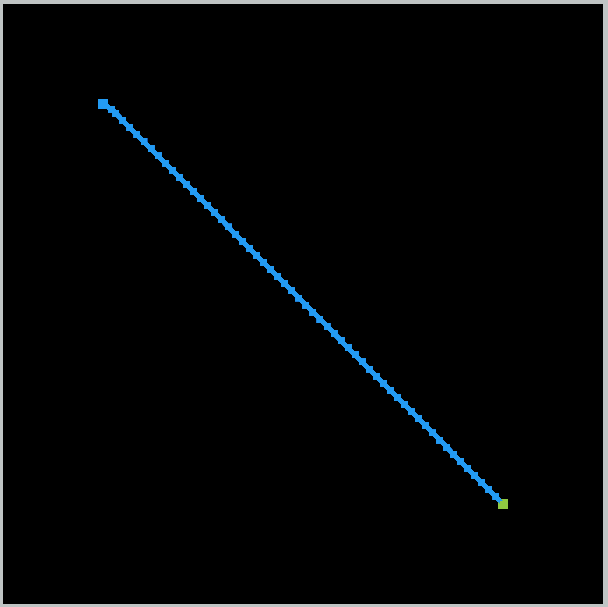
Demo
| Empty | Obstacle Map |
|---|---|
 |  |
| Iterations: 1 | Iterations: 1279 |
As we can see from the demo, with no obstacle, the algorithm is able to find a path directly to the goal. And with obstacles, the search attempts are still more concentrated toward the goal than the RRT. However, even with a faster searching ability, RRT-connect still does not give optimal solutions.
RRT*
RRT* is an optimized version of RRT, which is provably asymptotically optimal,
- Paper on RRT* in robotic motion planning: Anytime Motion Planning using the RRT*
- Original paper: Sampling-based Algorithms for Optimal Motion Planning
- Here is great YouTube video explaining the RRT* algorithm.
Pseudocode
- RRT_star works similarly to RRT, but after finding the new configuration $q_{new}$, we will check in the neighborhood, namely the K-Nearest-Neighbors, which one has the lowest cost to the $q_{new}$, and choose that neighbor to be its parent.
- Then, in reverse, take the new configuration $q_{new}$ as the parent, and compare the costs to the configurations in the neighborhood. If take $q_{new}$ as the new parent has a lower cost, then assign $q_{new}$ to be the new parent to them.
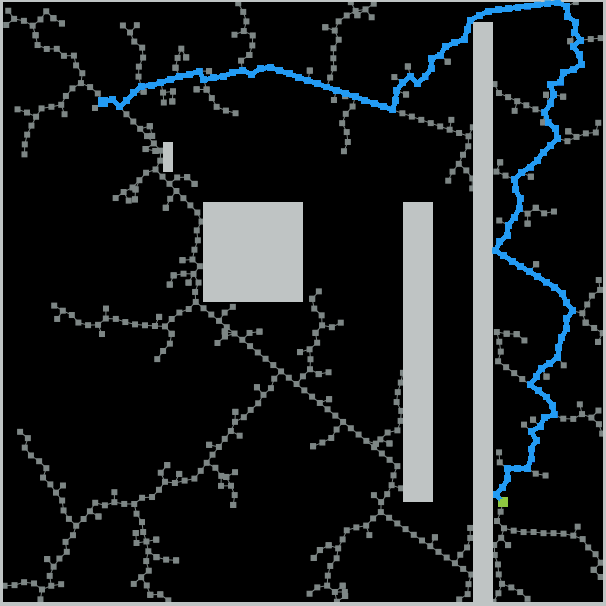
Demo
| Empty | Obstacle Map |
|---|---|
 |  |
| Iterations: 748 | Iterations: 7858 |
Comparing the search map between RRT* and RRT, we can clearly see that RRT* has cleaner branches because it keeps updating the parent-child relations.